10  Analiza varijanse (ANOVA)

10.1 Povratak na (diskretne) grupe

Vreme je da se vratimo na jedan od fundamentalnih problema statističke analize – poređenje između grupa koje su određene prema diskretnim obeležjima. Kada kažem diskretnim, mislim na to da su naše jedinice uzorka podeljene prema nekim jasnim kategorijama. Zašto je ovo važno? Zato što je ovo jedan od najčešćih scenarija u praksi.

Klasičan primer u društvenim istraživanjima je podela ispitanika na osnovu biološkog pola, što smo već videli kod t-testa. Drugi sjajan primer je obrazovanje. Gotovo svaki obrazovni sistem na svetu deli obrazovanje na osnovno, srednje i visoko. Ovo je primer ordinalne merne skale - svaka naredna kategorija označava viši stepen obrazovanja.

Hajde da odmah skočimo u konkretan primer koji će nam pomoći da razumemo zašto je ova tema važna. Zamislimo da istražujemo cene kafe u Novom Sadu. Imamo podatke o cenama iz XX kafeterija i znamo u kom delu grada se svaka nalazi. Grad je podeljen na tri zone:

  1. Uži centar (područje oko Zmaj Jovine, Dunavske, Pozorišnog trga)
  2. Širi centar (Grbavica, Liman, Sajam, Bulevar)
  3. Nova naselja (Detelinara, Novo Naselje, Telep, Satelit)

Ako nas zanima da proverimo da li prosečna cena kafe zavisi od lokacije kafterije, možemo da primenimo ono što smo dobro savladali – t-test. Međutim, potrebna su nam tri t-testa da bismo utvrdili da li postoji razlika između svake dve grupe.

  1. Uži centar vs. Širi centar
  2. Uži centar vs. Nova naselja
  3. Širi centar vs. Nova naselja

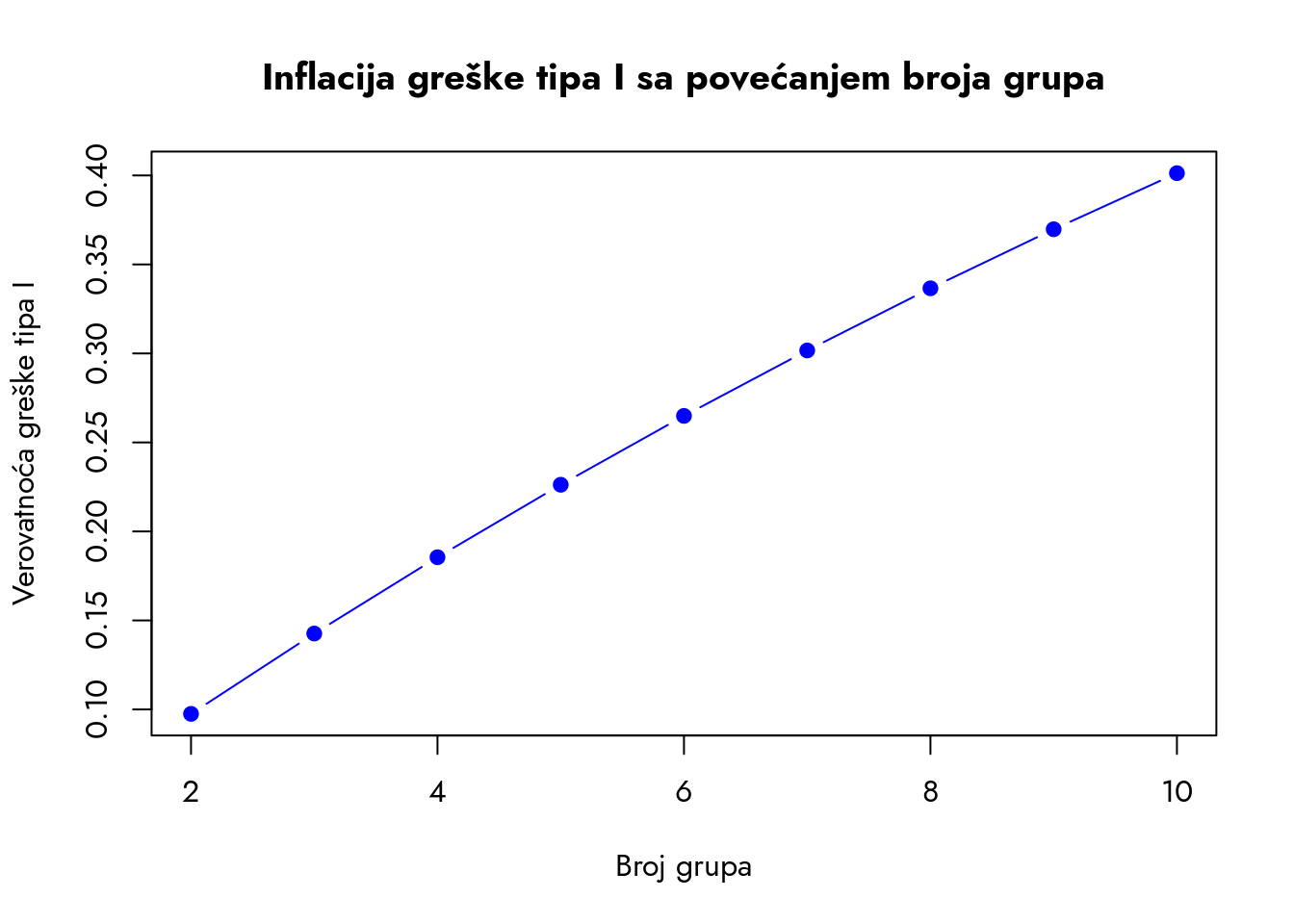
Dakle, trebaju nam tri zasebna zaključka na osnovu tri različita testa da bismo odgovorili na jedno pitanje. Sa druge strane, pitanje koje nas zanima je jednostavno – da li postoji zavisnost ili uticaj lokacije na cenu kafe? Korišćenje tri testa za odgovor na jedno pitanje čini se kao previše posla. Pri tome, ne zaboravimo da su to statistički testovi - svaki do njih poseduje rizik greške tipa I i tipa II. Ako povećavamo broj testova, povećavamo i rizik greške tipa I.

Razmislite, ako razlike na nivou populacije postoje između sve tri grupe, potrebno je da ispravno odbacimo tri različite nulte hipoteze. Ako je pri riziku greške od 5% verovatnoća da ćemo pri svakom testu ispravno odbaciti nultu hipotezu 95%, onda je verovatnoća da ćemo uspeti u svim tri testa \(95\% \times 95\% \times 95\% = 85.7\%\). Dakle, rizik greške tipa I se povećava sa brojem statističkih testova. Što je broj grupa za poređenje veći, to je veća verovatnoća da doneti ispravan zaključak kada objedinimo sve rezultate. Ovaj fenomen se naziva inflacija greške tipa I.

Inflacija greške tipa I sa povećanjem broja grupa

Šta je alternativa ovakvom pristupu? Potreban nam je novi metod koji će nam omogućiti da jednim udarcem rešimo problem poređenja više grupa. Međutim, postoji jedan veliki problem koji treba prevazići u ovom pristupu. Kada imamo više grupa, nije najjasnije razdvojiti razlike u podacima koje proističu iz različitih izvora.

10.2 Dva izvora varijabiliteta

Zamislite sledeću situaciju: dva studenta raspravljaju o cenama kafe. Prvi tvrdi: „U centru je kafa uvek skuplja nego u novim naseljima“. Drugi odgovara: „Ma nije to tako jednostavno. Poznajem jeftine kafiće u centru, a neki lanci su skupi gde god da se nalaze.“

Ova rasprava savršeno ilustruje dva ključna koncepta koja moramo razumeti:

  1. Varijabilitet između grupa (prvi student)
  2. Varijabilitet unutar grupa (drugi student)

Hajde da pažljivo analiziramo ovaj drugi argument. Saznajemo dve stvari:

  • Među kafićima u centru postoje značajne varijacije u ceni kafe
  • Postoji neki faktor koji nismo razmotrili (npr. da li je to lokalni kafe ili lanac kafeterija), a koji utiče na cenu kafe

Ova dva studenta zapravo opisuju dva izvora varijabiliteta u podacima.

  1. Prvi student opisuje varijabilitet između grupa - razlike u prosečnim cenama kafe između različitih delova grada.
  2. Drugi student opisuje varijabilitet unutar grupa - razlike u cenama kafe unutar samih grupa. Ovo nisu razlike između aritmetskih sredina, već razlike između pojedinačnih opservacija unutar iste grupe.

Oba tipa varijabiliteta su usko povezana sa podelom na grupe koje smo konstruisali. Razlike između grupa su posledica uticaja obeležja na osnovu kojih smo podelili jedinice uzorka u grupe. Ako između različitih delova grada postoje razlike u ceni kafe, to znači da nešto u tim delovima grada ostvaruje uticaj i pravi razliku u prosečima.

Problem u statističkoj analizi je što u svakom setu podataka mi možemo veoma lako pronaći i jedne i druge razlike. Hajde da vidimo kako to izgleda na našem primeru sa kafama. Hajde da vidimo kako izgleda distribucija cena kafe u kafeterijama u centru i novim naseljima.

Prvo učitavamo podatke.

  cena    lokacija
1  264 Širi centar
2  297 Širi centar
3  476 Širi centar
4  327 Širi centar
5  333 Širi centar
6  492 Širi centar

Zatim ćemo za svaku grupu podataka nacrtati histogram distribucije cena kafe.

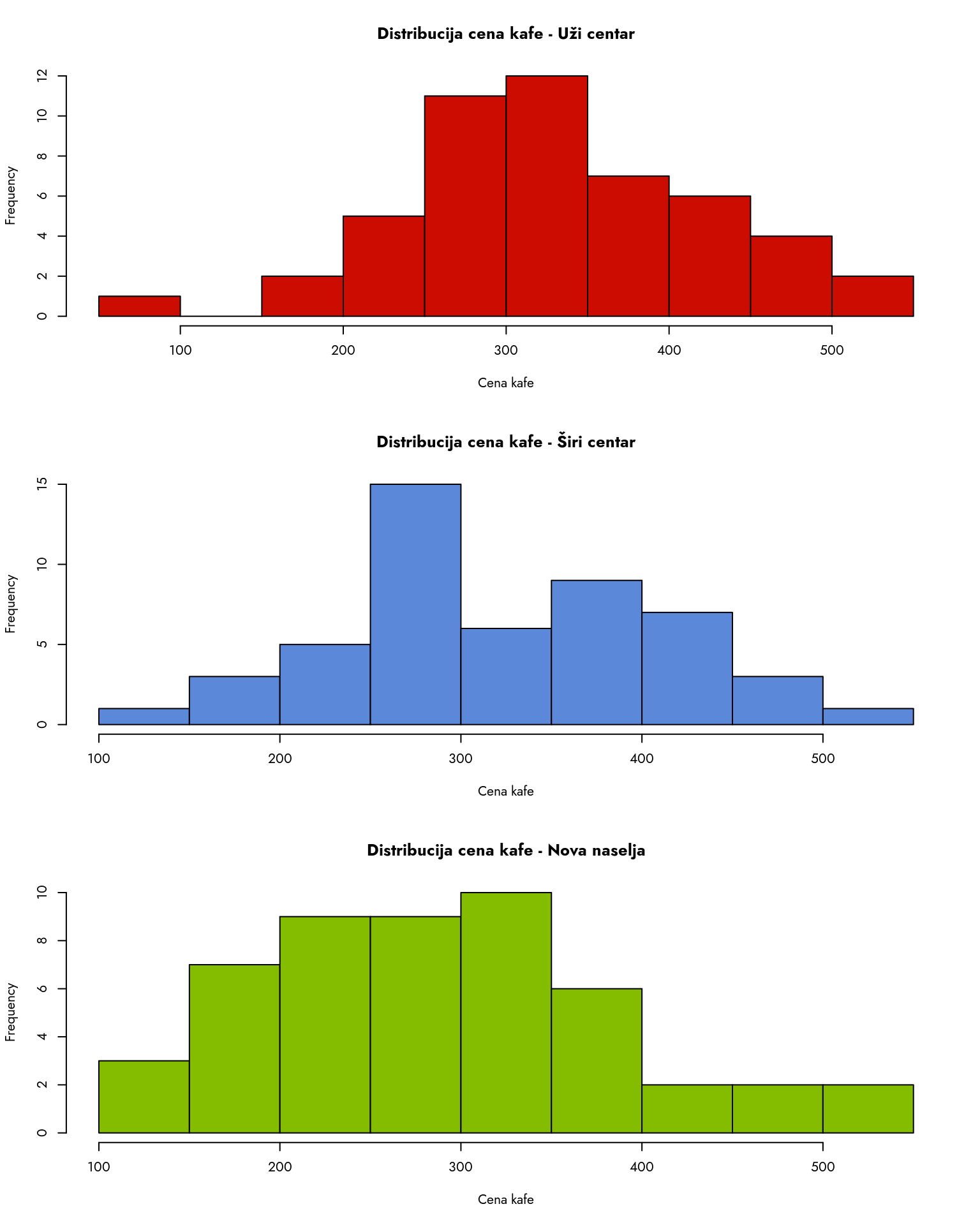
Distribucija cena kafe po lokaciji
  1. Podešavamo raspored grafikona na 3 reda i 1 kolonu
  2. Crtamo histogram za cene kafe u Užem centru
  3. Crtamo histogram za cene kafe u Širem centru
  4. Crtamo histogram za cene kafe u Novim naseljima

Na osnovu histograma možemo videti da postoji značajna varijabilnost u cenama kafe unutar svake grupe, što ide u prilog tezi koju zagovara student. U centru grada možete popiti kafu i za 100 dinara (ako znate gde da je pronađete) i za 500 dinara.

Međutim, vidimo i da između grupa postoje razlike u cenama kafe. Kafu za manje od 200 dinara je laše naći u novim naseljima nego u centru. Hajde da vidimo da li se to ogleda i u aritmetičkim sredinama.

Prikaži kod 
AS_siri_centar <- mean(podaci$cena[podaci$lokacija == "Širi centar"])

AS_uzi_centar <- mean(podaci$cena[podaci$lokacija == "Uži centar"])

AS_nova_naselja <- mean(podaci$cena[podaci$lokacija == "Nova naselja"])

cat("Aritmetička sredina cena kafe u Širem centru: ", round(AS_siri_centar, 2), "\n")

cat("Aritmetička sredina cena kafe u Užem centru: ", round(AS_uzi_centar, 2), "\n")

cat("Aritmetička sredina cena kafe u Novim naseljima: ", round(AS_nova_naselja, 2), "\n")
Aritmetička sredina cena kafe u Širem centru:  323.38 
Aritmetička sredina cena kafe u Užem centru:  330.64 
Aritmetička sredina cena kafe u Novim naseljima:  286.64

Vidimo da je prosečna cena kafe u Širem centru najviša (oko 330 dinara), dok je najniža u Novim naseljima (oko 286 dinara). Međutim, da li nas proseci varaju? Da li su razlike između grupa veće nego što su razlike unutar grupa? Koji student je u pravu?

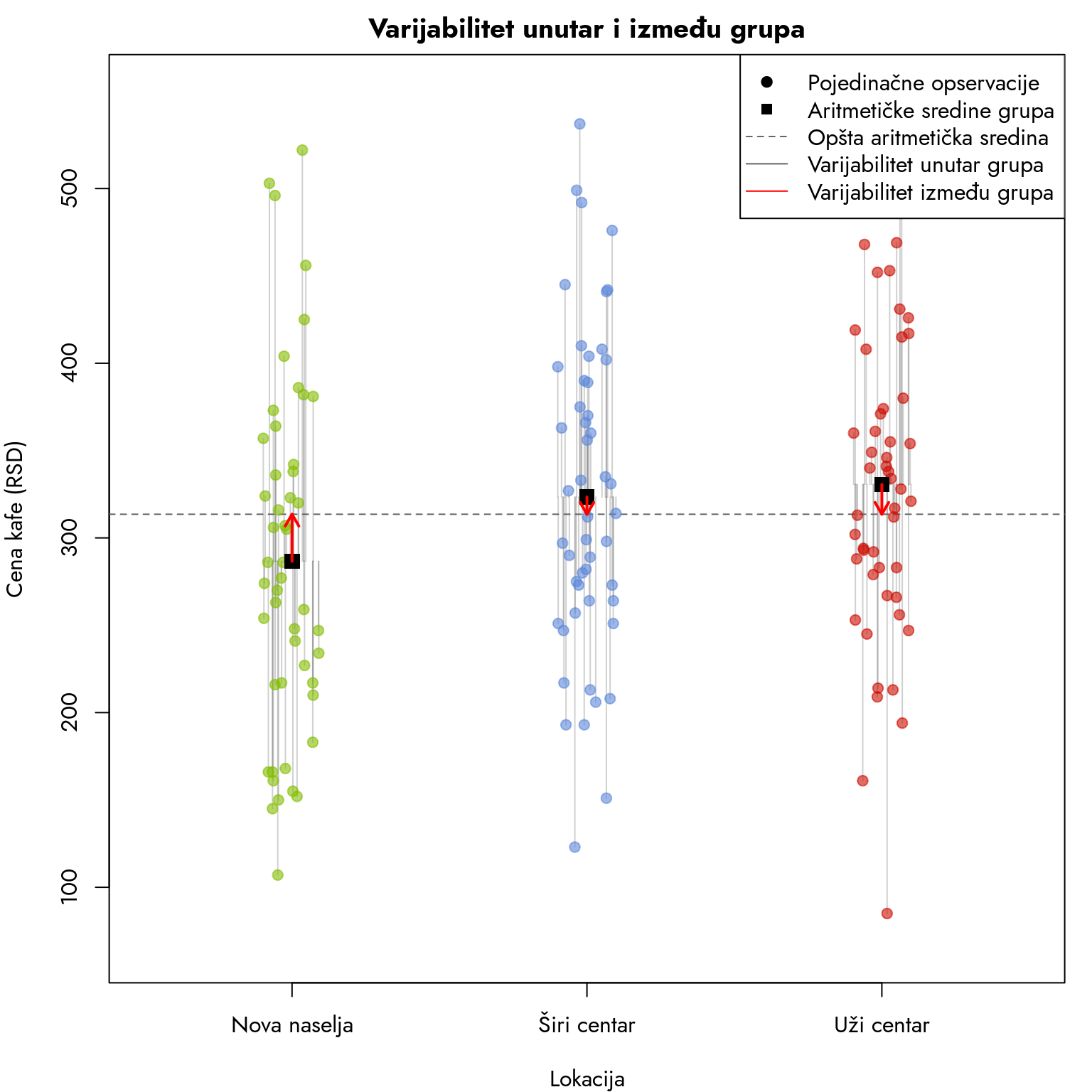
Hajde da pokušamo da vizualizaujemo odnos između ovih razlika.

Slika 10.1: Varijabilitet unutar i između grupa

Šta vidimo na ovom grafikonu? Svaka od tačaka predstavlja jednu opservaciju, tj. jednu zabeleženu cenu kafe u različitim delovima grada. Crni kvadrati predstavljaju aritmetičku sredinu svake grupe. Unutar svake grupe vidimo da su opservacije udaljene različito od proseka svoje grupe.

Međutim, vidimo da su i proseci svake grupe udaljeni od opšteg proseka (isprekidana horizontalna linija) i te udaljenosti su predstavljene crvenim linijama sa strelicom.

Na prvi pogled deluje da je situacija veoma jednostavna. Sive linije koje označavaju udaljenost opservacija od svojih grupa su značajno duže od malih crvenih linija. Međutim, ako želimo zaista da na osnovu ovih podataka donesemo zaključak, potrebno je da kvantifikujemo ovu razliku. Takođe, potrebno je da ovim izvorima varijabiliteta dodelimo „službena“ imena: faktorski i rezidualni varijabilitet.

10.3 Faktorski i rezidualni varijabilitet

Varijabilitet između grupa nazivamo faktorski varijabilitet. Ovaj varijabilitet je posledica razlika između grupa koje su definisane na osnovu nekog faktora. U našem slučaju, faktor je lokacija kafeterije. Faktori su veoma česti naziv za nezavisne varijable koje su merene kategorijalno, tj. nominalnom ili ordinalnom mernom skalom.

Faktorski varijabilitet je predmet našeg istraživanja. Na kraju, definisali smo i iskoristili varijablu lokacija kako bismo ispitali uticaj lokacije na cenu kafe. Taj uticaj se manifestuje kroz faktorski varijabilitet.

Slika 10.1 daje privid da je rezidualni varijabilitet značajno veći, sudeći po dužini i broju sivih linija. Međutim, taj vizuelni utisak može lako da nas prevari. Zašto? Ova dva tipa varijabiliteta nisu direktno uporedivi jer poseduju različite cdstepene slobode.

Stepene slobode upoznali smo kada smo govorili o t-testu (Odeljak 7.2). Oni predstavljaju odnos između broj opservacija i broja nepoznatih parametara.

U slučaju faktorskog varijabiliteta, broj stepeni slobode je jednak broju grupa minus jedan. Zašto baš ovako? Ovo je situacija koja je analogna problemu sa tri kese koji smo spominjali ranije. Imamo tri aritmetičke sredine grupa i imamo opštu aritmetičku sredinu varijable cena koja predstavlja nepoznati parametar. Samim tim, broj stepeni slobode biće: \(df_F = k - 1 = 3-1 = 2\), gde je \(k\) broj grupa.

Sa druge strane, kod rezidualnog varijabiliteta broj stepeni slobode je jednak broju opservacija minus broj grupa. U ovom slučaju sve opservacije čine naš uzorak, a imamo tri nepoznata parametra - aritmetičke sredine grupa. Dakle, broj stepeni slobode za rezidualni varijabilitet je: \(df_R = N - k\), gde je \(N\) ukupan broj opservacija, a \(k\) broj grupa. U našem slučaju imamo 150 opservacija i 3 grupe, pa je \(df_R = 150 - 3 = 147\). Kao što možemo videti, broj stepeni slobode će uvek biti značajno veći u slučaju rezidualnog varijabiliteta.

U oba slučaja broj nepoznatih parametara označava broj aritmetičkih sredina u odnosu na koje posmatramo razlike, tj. varijabilitet. U prvom slučaju je to jedna aritmetička sredina, a u drugom su to aritmetičke sredine svake grupe.

OK, sada kada znamo šta su faktorski i rezidualni varijabilitet, hajde da vidimo kako možemo da ih kvantifikujemo i uporedimo. Metod koji se koristi za ovu svrhu naziva se analiza varijanse ili skraćeno ANOVA.

10.4 ANOVA postupak

Postupak izračunavanja varijabiliteta smo ranije videli kod primera izračunavanja varijanse, kovarijanse i greške regresije. Sada ćemo primeniti sličan postupak, ali na grupisane podatke.

Počećemo od faktorskog varijabiliteta. On predstavlja udaljenost aritmetičkih sredina grupa od opšte aritmetičke sredine. Faktorski varijabilitet je u svojoj suštini izražen kroz kvadrirano odstupanje svake aritmetičke sredine od opšte aritmetičke sredine svih opservacija. Ovaj tip varijabiliteta kvantifikujemo putem sledeće formule:

\[ SS_F = \sum_{i=1}^{k} n_i (\overline{X}_i - \overline{X})^2 \]

gde je \(SS_F\) faktorski varijabilitet, \(n_i\) broj opservacija u \(i\)-toj grupi, \(\overline{X}_i\) aritmetička sredina \(i\)-te grupe, a \(\overline{X}\) opšta aritmetička sredina svih opservacija. U formuli vidimo da se kvadrat razlike između aritmetičke sredine grupe i opšte aritmetičke sredine množi sa brojem opservacija u grupi. Ovakav pristup ima svoju logiku - veće grupe nam daju više informacija o odnosu između proseka te grupe i opšteg proseka. Koristimo oznaku \(SS_F\) da naglasimo da računamo sumu kvadriranih odstupanja, što je osnovni princip izračunavanja varijabiliteta kvantitativnih varijabli.

Rezidualni varijabilitet, sa druge strane, predstavlja sumu kvadrata odstupanja svake opservacije od aritmetičke sredine svoje grupe. Izračunavamo ga pomoću formule:

\[ SS_R = \sum_{i=1}^{k} \sum_{j=1}^{n_i} (X_{ij} - \overline{X}_i)^2 \]

Ovaj izraz izgleda komplikovano zbog dvostrukog sumiranja \(\sum_{i}^k\) i \(\sum_{j}^{n_i}\). Prvi indeks sumiranja prolazi kroz sve grupe, dok drugi indeks sumira sve opservacije unutar svake grupe. Suština rezidualnog varijabiliteta ogleda se u procesu koji ima dva koraka:

  1. prolazimo kroz svaku grupu posebno \(\sum_{i}^k ...\),
  2. unutar svake grupe prolazimo kroz sve opservacije \(\sum_{j}^{n_i} ...\) i računamo kvadrat odstupanja te opservacije od aritmetičke sredine svoje grupe \(X_{ij} - \overline{X}_i\).

Hajde da demonstriramo izračunavanje oba tipa varijabiliteta u R-u.

Prikaži kod 
# Izračunavanje faktorskog varijabiliteta

opsta_sredina <- mean(podaci$cena)

sredine_grupa <- c(AS_nova_naselja, AS_siri_centar, AS_uzi_centar)

velicine_grupa <- table(podaci$lokacija)

SSF <- sum(velicine_grupa * (sredine_grupa - opsta_sredina)^2)

cat("Faktorski varijabilitet: ", round(SSF, 2), "\n")
1
Izračunavamo opštu aritmetičku sredinu svih opservacija
2
Spajamo aritmetičke sredine grupa u jedan vektor
3
Iz tabulacije varijable lokacija dobijamo veličine grupa u jednom vektoru
4
Izračunavamo faktorski varijabilitet prema formuli koju smo videli ranije 
Faktorski varijabilitet:  55642.25

Kao i svaka druga suma kvadrata, faktorski varijabilitet nam ne daje direktno interpretabilnu vrednost.

Sada prelazimo na izračunavanje rezidualnog varijabiliteta. Da bismo to uradili precizno i metodično, prvo ćemo razdvojiti podatke po grupama.

Prikaži kod 
# Izdvajanje podataka po grupama

uzi_centar <- podaci$cena[podaci$lokacija == "Uži centar"]

siri_centar <- podaci$cena[podaci$lokacija == "Širi centar"]

nova_naselja <- podaci$cena[podaci$lokacija == "Nova naselja"]

SSR <- sum((uzi_centar - AS_uzi_centar)^2) + sum((siri_centar - AS_siri_centar)^2) + sum((nova_naselja - AS_nova_naselja)^2)

cat("Rezidualni varijabilitet: ", round(SSR, 2), "\n")
1
Izdvajamo cene kafe po grupama
2
Izračunavamo rezidualni varijabilitet prema formuli iznad 
Rezidualni varijabilitet:  1302325

Rezidualni varijabilitet u našem primeru je takođe velika cifra, ali kao i faktorski varijabilitet, nema direktnu interpretaciju. Kao što smo već naglasili, ova dva varijabiliteta ne možemo direktno porediti. Da bismo ih mogli uporediti, potrebno je da ih transformišemo u faktorsku i rezidualnu varijansu.

U toku ovog udžbenika naizmenično smo koristili pojmove varijabiliteta i varijanse. U pretposlednjem poglavlju važno je da napravimo formalnu razliku između ova dva pojma, jer oni nisu sinonimi.

Varijabilitet ili varijabilnost je osnovna karakteristika skupa podataka koja opisuje koliko su podaci raspršeni oko neke centralne vrednosti. Kada govorimo o „sirovom“ varijabilitetu, mislimo na jednu od dve stvari:

  1. Sumu apsolutnih odstupanja od centralne vrednosti (npr. aritmetičke sredine)
  2. Sumu kvadrata odstupanja od centralne vrednosti

U oba slučaja varijabilitet predstavlja sumu odstupanja od centralne tendencije. Najčešće koristimo sumu kvadriranih odstupanja, pa ove osnovne mere varijabilnosti nazivamo sumama kvadrata.

Varijansa je specifična transformacija ovog sirovog varijabiliteta. Ona predstavlja odnos između varijabiliteta (sume kvadrata odstupanja) i odgovarajućih stepeni slobode. Preciznije, varijansa je prosečno kvadratno odstupanje po stepenu slobode i dobijamo je deljenjem sume kvadrata sa brojem stepeni slobode. Na ovaj način dobijamo međusobno uporedive mere varijabiliteta za grupe različitih veličina.

Logika ove razlike je slična tome zašto ne koristimo sumu svih vrednosti da opišemo centralnu tendenciju varijable, već koristimo aritmetičku sredinu. Same sume (vrednosti, apsolutnih vrednosti ili kvadriranih vrednosti) daju brojeve koje ne možemo smisleno interpretirati niti uporediti jer direktno zavise od veličine uzorka.

Da bismo došli do faktorske i rezidualne varijanse, faktorski i rezidualni varijabilitet delimo sa odgovarajućim stepenima slobode.

\[\begin{align} s_F &= \frac{SS_F}{df_F} \\ s_R &= \frac{SS_R}{df_R} \end{align}\]

Hajde da vidimo kako to izgleda u R-u.

Prikaži kod 
sF <- SSF / (3-1)
sR <- SSR / (150-3)

cat("Faktorska varijansa: ", round(sF, 2), "\n")
Faktorska varijansa:  27821.13
Prikaži kod 
cat("Rezidualna varijansa: ", round(sR, 2), "\n")
Rezidualna varijansa:  8859.35

Sada imamo međusobno uporedive vrednosti. Faktorska varijansa iznosi približno 28000, dok rezidualna varijansa iznosi približno 8900. Na osnovu ovoga možemo zaključiti da je na nivou našeg uzorka faktorska varijansa značajno veća od rezidualne, tj. da su razlike između grupa mnogo izraženije nego razlike unutar grupa. Ako je verovati našem uzorku, prvi student je bio u pravu.

Da bismo upotpunili naše razumevanje varijabiliteta, pogledajmo i kolika je varijansa same varijable koja meri cenu kafe.

Varijansa cene kafe:  9113.87

U kakvom odnosu je ova ukupna varijansa sa faktorskom i rezidualnom varijansom? Ako saberemo faktorski i rezidualni varijabilitet, dobićemo ukupan varijabilitet. Kada taj ukupan varijabilitet podelimo sa brojem stepeni slobode za ocenu varijanse uzorka (\(N-1\)), dobićemo upravo varijansu čitave varijable cena. Dakle, vrednost koju smo dobili direktnim izračunavanjem varijanse je zapravo kombinovani zbir faktorske i rezidualne varijanse.

Prikaži kod 
SSU <- SSF + SSR

s2 <- SSU / (150 - 1)

cat("Ukupan varijabilitet: ", round(SSU, 2), "\n")

cat("Varijansa cene kafe: ", round(s2, 2), "\n")
1
Izračunavamo ukupan varijabilitet kao zbir faktorskog i rezidualnog varijabiliteta
2
Izračunavamo varijansu cene kafe kao ukupan varijabilitet podeljen sa brojem stepeni slobode 
Ukupan varijabilitet:  1357967 
Varijansa cene kafe:  9113.87

Kao što vidite dobili smo identičan broj. Ovaj proces izračunavanja faktorskog i rezidualnog varijabiliteta naziva se dekompozicija ili razlaganje varijanse. Sam metod koji ćemo uskoro upoznati zove se analiza varijanse upravo zato što razdvaja ukupnu varijansu na onu koju proizvodi faktor i onu koja ostaje unutar grupa.

Koji je cilj ovakve analize? Želimo da utvrdimo koliko je puta faktorska varijansa veća od rezidualne. Taj odnos faktorske i rezidualne varijanse naziva se F-statistika i predstavlja osnovu za testiranje statističke značajnosti faktorskog varijabiliteta.

\[ F = \frac{s_F}{s_R} \]

Pre nego što objasnimo prirodu F-statistike, važno je naglasiti razliku u odnosu na t-statistiku. Ako pogledamo t-test za 2 uzorka, nulta hipoteza je fokusirana na vrednost 0 unutar t-distribucije jer nula označava odsustvo razlika između grupa, pa samim tim i odsustvo efekta. Kod F-statistike situacija je drugačija - ne očekujemo vrednost 0. Zašto? Pošto je F-statistika količnik mera varijabiliteta, ona može biti bilo koja pozitivna vrednost. Nula ne predstavlja samo odsustvo efekta, već potpuno odsustvo varijabiliteta iz faktora, što je izuzetno retko u empirijskim istraživanjima.

Ključna vrednost za razumevanje ove statistike je \(F=1\). Ako je F-statistika jednaka 1, to znači da je faktorska varijansa jednaka rezidualnoj varijansi - razlike između grupa su jednake razlikama unutar grupa. Ako je F-statistika veća od 1, faktorska varijansa nadmašuje rezidualnu varijansu, što znači da su razlike između grupa izraženije od razlika unutar grupa. Suprotno tome, F-statistika manja od 1 ukazuje da su razlike unutar grupa dominantnije od razlika između grupa, što odgovara scenariju odsustva efekta.

Dakle, da bismo demonstrirali postojanje statistički značajnog efekta faktora na nivou populacije, F mora prevazići vrednost 1, pokazujući da faktorska varijansa nadmašuje rezidualnu varijansu. Koliko velika F-statistika mora biti? Odgovor na ovo pitanje leži u još jednoj distribuciji verovatnoće - F-distribuciji.

10.5 F-distribucija

Pre nego što vidimo F-distribuciju na delu, važno je istaći po čemu se ona suštinski razlikuje od normalne i t-distribucije. Kada pogledamo formulu za F-statistiku, uočićemo jednu fundamentalnu činjenicu - F-statistika je uvek pozitivan broj. Pošto predstavlja količnik dve varijanse, matematički je nemoguće da bude negativna.

Kroz F-distribuciju pokušavamo da opišemo situaciju koja odgovara nultoj hipotezi i odsustvu efekta. U tom slučaju, najveća koncentracija verovatnoće nalazi se između 0 i 1 (analogno vrednosti 0 u t-distribuciji). U odnosu na ovu vrednost, F-distribucija pokazuje jasnu asimetriju u desno, što znači da ekstremne vrednosti nalazimo isključivo na desnoj strani distribucije.

Šta je logika ove asimetrije? Ponovo, odgovor leži u prirodi F-statistike. Kada pretpostavljamo odsustvo efekta, očekujemo vrednosti manje od ili jednake 1, jer to znači da je faktorski varijabilitet jednak ili manji od rezidualnog. Značajno veći faktorski varijabilitet predstavlja direktan dokaz protiv nulte hipoteze, zbog čega distribucija mora biti asimetrična u desno.

Kao i t-distribucija, F-distribucija mora biti adaptivna prema karakteristikama uzorka koji analiziramo. U ovom slučaju imamo dva ključna parametra koja oblikuju F-distribuciju: broj stepeni slobode faktora i broj stepeni slobode reziduala. Promena ovih parametara direktno utiče na oblik F-distribucije.

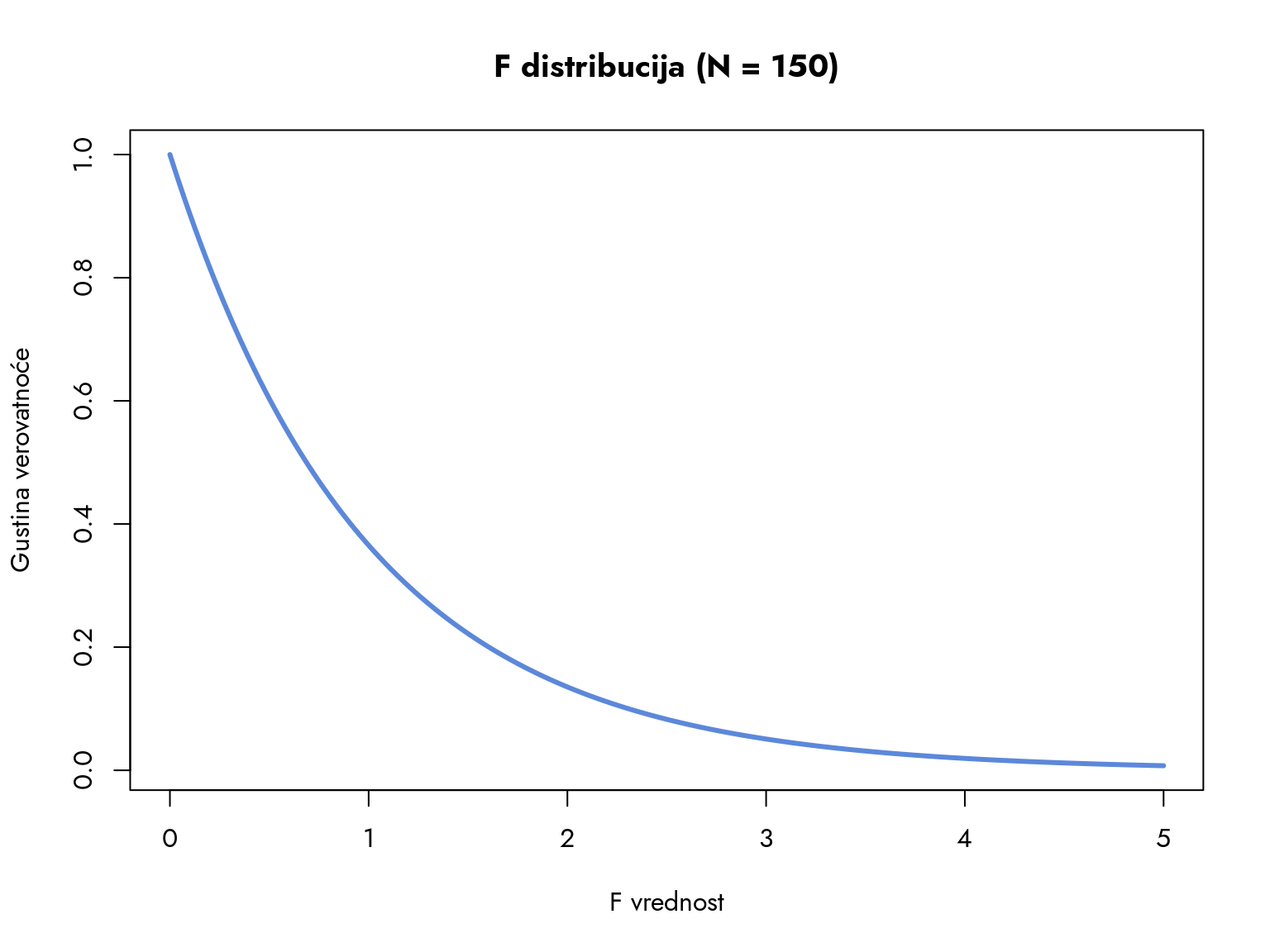
Hajde da vizualizujemo kako bi izgledala F-distribucija u našem primeru.

Prikaži kod 
par(family = "Jost")
df1 <- 2
df2 <- 150 - 3

x <- seq(0, 5, length.out = 200)

y <- df(x, df1, df2)

plot(x, y, type = "l", lwd = 3, col = "#5C88DAFF",
     xlab = "F vrednost", 
     ylab = "Gustina verovatnoće",
     main = "F distribucija (N = 150)")
1
Broj stepeni slobode faktora
2
Broj stepeni slobode reziduala
3
Generišemo vrednosti za x-osu; uzimamo samo pozitivne vrednosti
4
Izračunavamo gustinu verovatnoće za svaku vrednost x pomoću ugrađene funkcije df koja računa gustinu verovatnoće F-distribucije
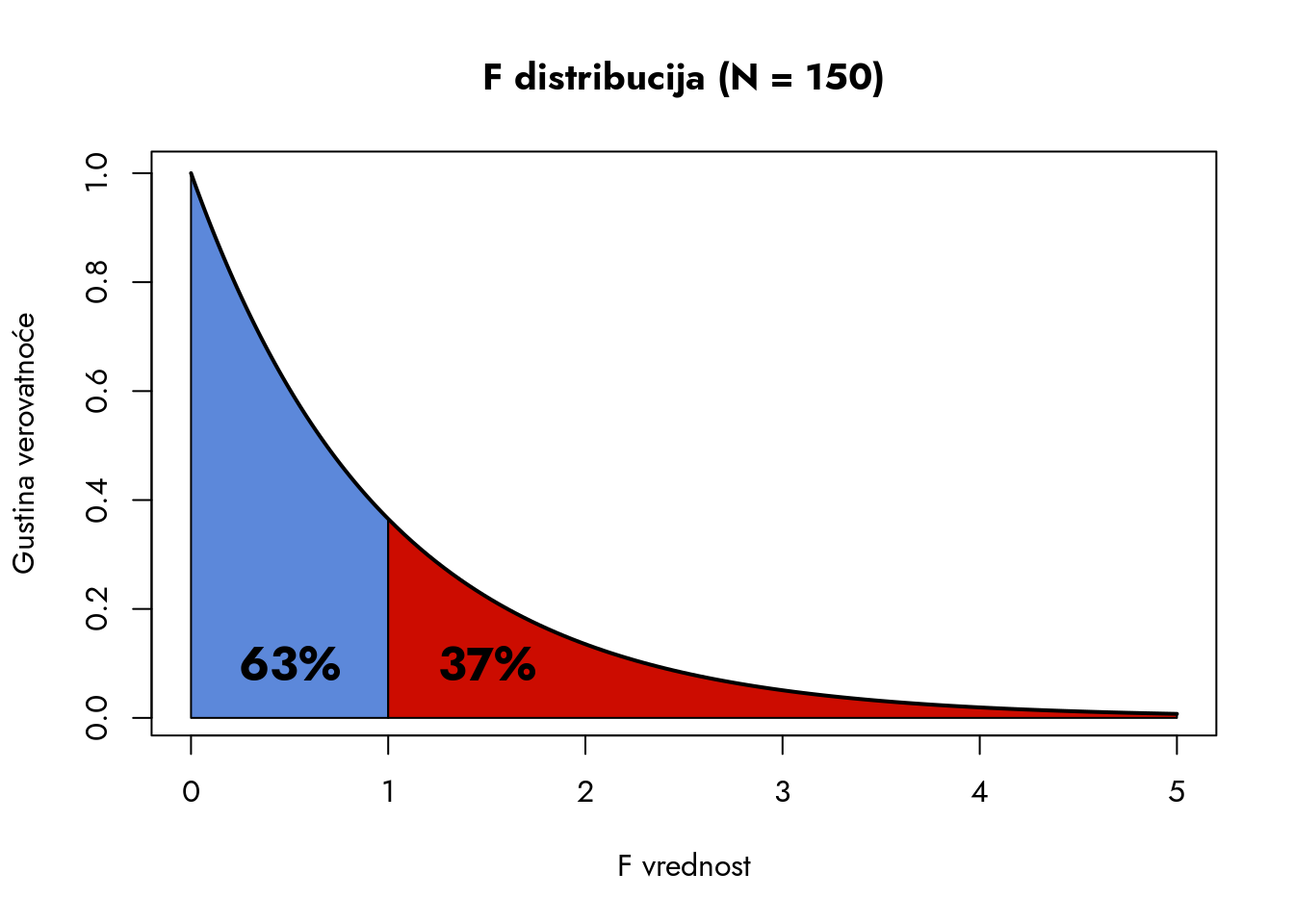
Slika 10.2: F distribucija za N=150 opservacija

Vidimo da se najveća koncentracija vrednosti nalazi između 0 i 1. Razmotrimo sada koliki deo površine ispod krive zauzima interval od 0 do 1, a koliki deo se nalazi desno od 1.

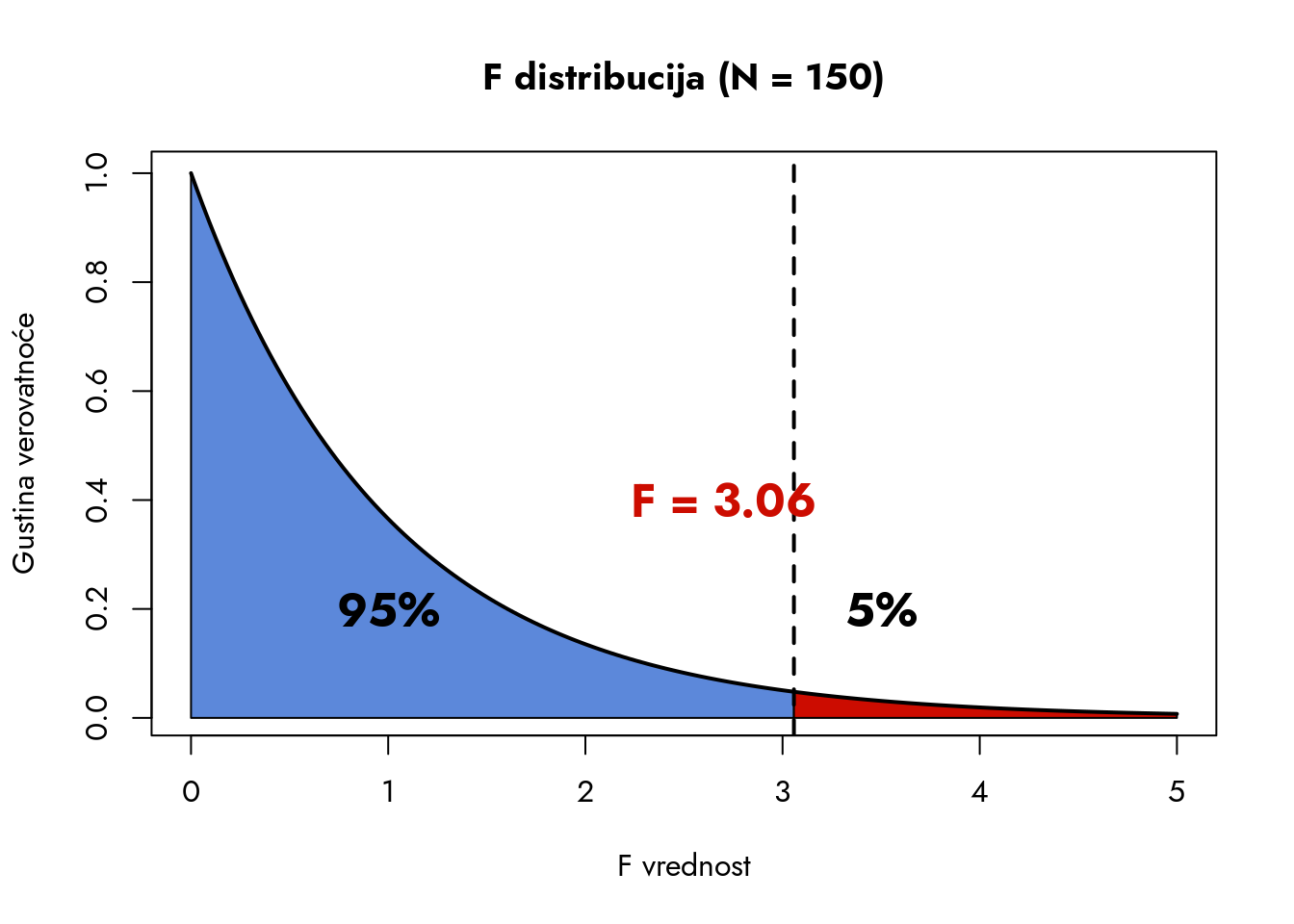
Slika 10.3: F distribucija sa označenim oblastima F < 1 i F > 1

Plavi deo obuhvata 63% svih mogućih F-statistika i predstavlja oblast koja je najkonzistentnija sa nultom hipotezom. Vrednosti F-statistike iznad 1 obuhvataju preostalih 37% svih mogućih vrednosti - ovo je oblast od posebnog interesa za našu analizu. Međutim, kao i kod drugih statističkih distribucija, fokusiramo se na površinu ispod krive koja sadrži mali procenat najekstremnijih vrednosti. Na primer, ako bismo želeli da pomerimo granicu udesno tako da plava oblast obuhvata 95% svih mogućih vrednosti, kolika bi trebalo da bude F-statistika?

Slika 10.4: F distribucija sa označenim kritičnim oblastima (95% i 5%)

Na grafikonu vidimo da je to vrednost \(F=3.06\). Dakle, da bismo na ovakvom uzorku i sa ovim brojem grupa mogli zaključiti da postoji značajan efekat faktora, faktorska varijansa mora biti približno tri puta veća od rezidualne. Ovo je kritična tačka koja razdvaja oblast u kojoj nemamo dovoljno dokaza protiv nulte hipoteze od oblasti u kojoj moramo odbaciti nultu hipotezu.

Sa samo tri grupe, F-distribucija ima oblik koji podseća na desni rep normalne distribucije. Međutim, promena broja grupa značajno utiče na oblik distribucije. Kako broj grupa raste, F-distribucija dobija svoj prepoznatljiv oblik - postaje sve više asimetrična i verovatnoća se koncentriše oko vrednosti 1.

Slika 10.5: F distribucija za različit broj grupa (N = 150)

Zašto dolazi do ovog pomeranja oblasti najveće koncentracije vrednosti udesno? Sa povećanjem broja grupa, faktički povećavamo i faktorski varijabilitet. Što je veći broj grupa, to više prostora imaju međugrupne razlike da dođu do izražaja, čak i kada je dejstvo faktora zanemarljivo. Zbog samog povećanja broja grupa koje poredimo, sredina distribucije pomera se ka 1, odnosno ka izjednačenom faktorskom i rezidualnom varijabilitetu.

Konačno, kada radimo sa velikim brojem grupa, F distribucija poprima oblik pozitivno asimetrične modifikacije normalne distribucije.

Sada smo spremni da pokrenemo formalnu ANOVA analizu. Najpre ćemo uvesti F-test i prikazati njegovu primenu u R-u.

10.6 F-test

Nulta hipoteza F-testa označava odsustvo dejstva nezavisne varijable (faktora) na zavisnu varijablu. Preciznije, nulta hipoteza tvrdi da ne postoji razlika između aritmetičkih sredina grupa. Pošto tih aritmetičkih sredina može biti 3, 5, 10 ili više, ovaj tip hipoteze nazivamo omnibus hipoteza. Sam termin potiče iz latinskog i znači „za sve“. U našem slučaju, nulta hipoteza tvrdi da je efekat faktora nepostojeći za sve grupe.

Alternativna hipoteza ima podjednako zanimljiv oblik. Šta bi bilo suprotno onome što predviđa nulta hipoteza? Dovoljno je da se samo jedna aritmetička sredina razlikuje od ostalih i već imamo osnovu za odbacivanje nulte hipoteze. Alternativna hipoteza F-testa tvrdi da postoji bar jedna grupa koja se razlikuje od ostalih. Ove hipoteze formalno zapisujemo na sledeći način:

\[\begin{align} H_0: \mu_1 = \mu_2 = \mu_3 = \ldots = \mu_k \\ H_1: \text{bar jedna } \mu_i \neq \mu_j \end{align}\]

Kada jedna grupa odstupa od ostalih, to direktno proizvodi značajan porast faktorskog varijabiliteta, što dovodi do veće vrednosti F statistike. Jednostavno rečeno, F-test proverava da li je faktorska varijansa dovoljno puta veća od rezidualne varijanse.

Razmotrimo rezultate koje smo dobili:

  • Faktorska varijansa: 2.782113^{4}
  • Rezidualna varijansa: 8859.35

Sledeći korak je izračunavanje F-statistike.

Prikaži kod 
F <- sF / sR

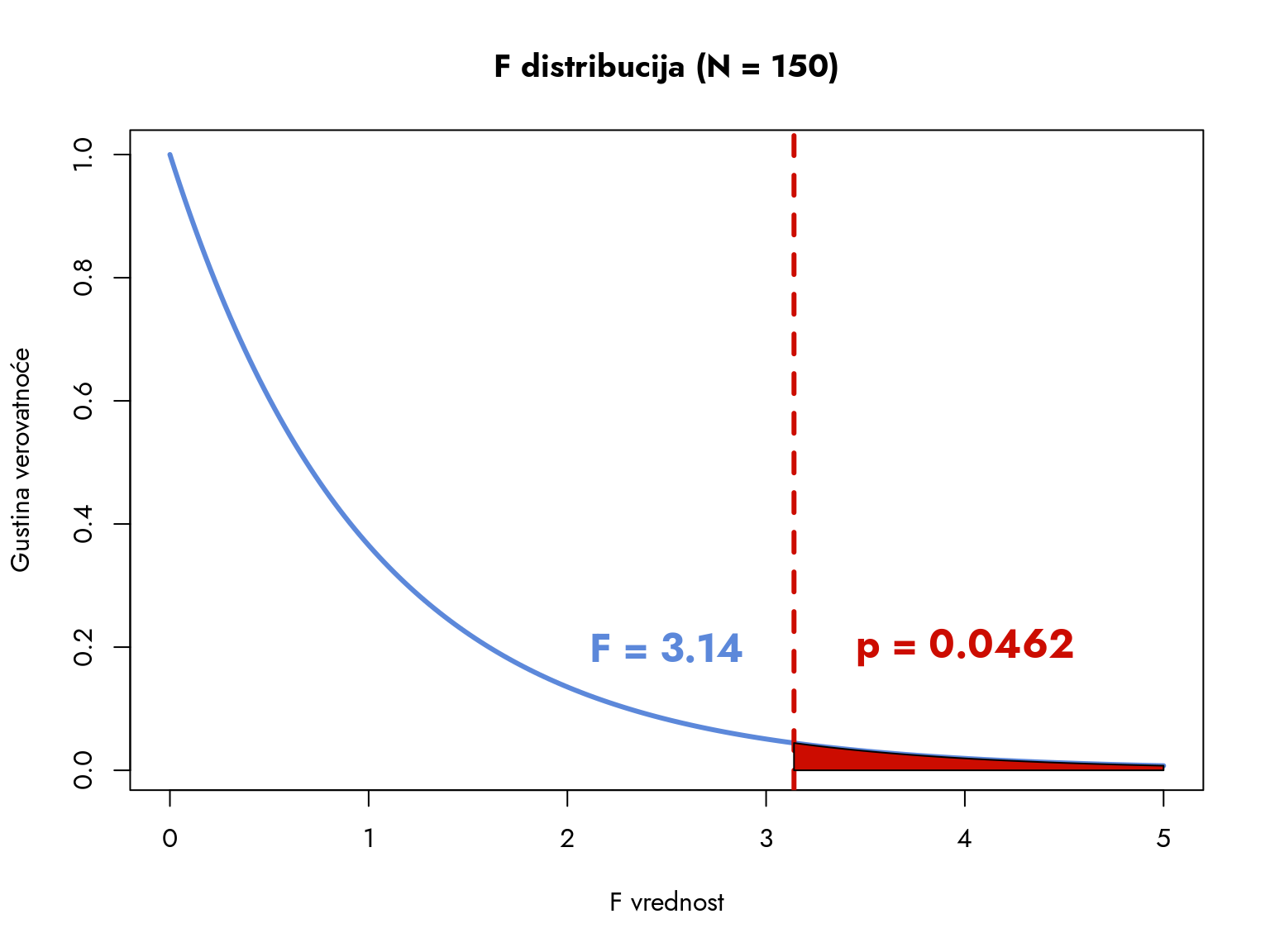
cat("F-statistika: ", round(F, 2), "\n")
F-statistika:  3.14

Sada ćemo vizuelno prikazati poziciju naše F-statistike u odnosu na F-distribuciju koja je definisana parametrima našeg primera - faktorskim stepenima slobode (2) i rezidualnim stepenima slobode (147, jer imamo 150 opservacija i 3 grupe).

Prikaži kod 
par(family = "Jost")

df1 <- 2 #<1
df2 <- 150 - 3

x <- seq(0, 5, length.out = 200)

y <- df(x, df1, df2)

plot(x, y, type = "l", lwd = 3, col = "#5C88DAFF",
     xlab = "F vrednost", 
     ylab = "Gustina verovatnoće",
     main = "F distribucija (N = 150)")

abline(v = F, lty = 2, lwd = 3, col = "#CC0C00FF")

text(2.5, 0.2, paste0("F = ", round(F, 2)), font = 2, cex = 1.5, col = "#5C88DAFF")

x_right <- seq(F, 5, length.out = 100)
y_right <- df(x_right, df1, df2)

polygon(c(x_right, 5, F), c(y_right, 0, 0), col = "#CC0C00FF")

p_value <- 1 - pf(F, df1, df2)

text(4, 0.2, paste0("p = ", round(p_value, 4)), font = 2, cex = 1.5, col = "#CC0C00FF")
1
Definišemo broj stepeni slobode faktora i reziduala
2
Generišemo vrednosti za x-osu. F-distribucija je definisana za vrednosti veće od 0
3
Izračunavamo gustinu verovatnoće prema F-distribuciji za svaku vrednost x koristeći ugrađenu funkciju df
4
Kreiramo grafikon F-distribucije
5
Dodajemo vertikalnu liniju koja označava vrednost F-statistike
6
Bojimo oblast desno od F-statistike
7
Izračunavamo p-vrednost kao površinu ispod krive desno od F-statistike korišćenjem ugrađene funkcije pf
Slika 10.6: F distribucija sa označenom vrednošću F-statistike

Vidimo da se naša F-statistika nalazi u desnom delu distribucije, što znači da je faktorska varijansa značajno veća od rezidualne. Da li je ta razlika dovoljno velika da bismo odbacili nultu hipotezu? To nam otkriva p-vrednost koja iznosi 0.0462. Ova vrednost nam pokazuje kolika je verovatnoća da dobijemo ovakvu ili ekstremniju vrednost F-statistike pod pretpostavkom da je nulta hipoteza tačna. Ta verovatnoća je u našem slučaju manja od 5%, odnosno \(p < 0.05\). To znači da posedujemo dovoljno dokaza da odbacimo nultu hipotezu i zaključimo da postoji bar jedna grupa koja se statistički značajno razlikuje od ostalih.

Praktično, veća vrednost F-statistike ukazuje na snažnije dejstvo faktora na zavisnu varijablu. Kada F-statistika premaši kritičnu vrednost, kao u našem primeru, možemo zaključiti da je efekat faktora statistički značajan.

Međutim, sama ANOVA nam ne otkriva koja grupa (ili grupe) se razlikuje od ostalih. Da bismo dobili precizniju sliku o prirodi ovih razlika, neophodno je sprovesti post-hoc analizu.

10.7 Post-hoc analiza

Naziv post-hoc nam govori da je reč o analizi koja se sprovodi nakon što dobijemo značajne rezultate ANOVA analize. Post-hoc analiza je niz testova koji se izvršavaju kada ANOVA test pokaže postojanje značajne razlike između grupa. Glavni cilj post-hoc analize je da precizno identifikuje koje grupe se međusobno razlikuju i kolika je veličina tih razlika. Na taj način dobijamo precizniju sliku o prirodi uticaja faktora na zavisnu varijablu.

Postoji nekoliko pristupa post-hoc analizi, a izbor zavisi od broja grupa, veličine uzorka i prirode podataka. U ovom udžbeniku predstavićemo jedan od najčešće korišćenih metoda - Tjukijev post-hoc test (Tukey, 1949). Ovaj test je efikasan i pruža sve ključne informacije o međugrupnim razlikama.

Tjukijev test spada u „konzervativne“ testove jer rešava problem višestrukog testiranja. Kada poredimo više grupa međusobno, povećavamo verovatnoću greške tipa I. Tjukijev test elegantno rešava ovaj problem korigujući nivo značajnosti za svako pojedinačno poređenje. Zato nosi i naziv Tjukijev test „poštenih značajnih razlika“ (engl. HSD – Honest Significant Differences).

Osnovni princip testa je sledeći: svaki par razlika između grupa poredi se sa kritičnom vrednošću određenom za taj specifični par. Matematička pozadina određivanja kritičnih vrednosti Tjukijevog kriterijuma je izvan okvira ovog udžbenika, ali u R-u možemo brzo i efikasno sprovesti i ANOVA analizu i Tjukijev post-hoc test.

U R-u, ANOVA analizu i Tjukijev post-hoc test izvršavamo pomoću funkcija aov i TukeyHSD. Pogledajmo kako to funkcioniše u praksi.

Prikaži kod 
anova_model <- aov(cena ~ lokacija, data = podaci)

summary(anova_model)
1
Prvo definišemo model pomoću funkcije aov. Model zadajemo u obliku zavisna_varijabla ~ faktor. U našem slučaju, zavisna varijabla je cena, a faktor je lokacija.
2
Funkcijom summary dobijamo sve relevantne informacije ANOVA analize. Posebno je važna poslednja kolona koja sadrži p-vrednost za F-test. 
             Df  Sum Sq Mean Sq F value Pr(>F)  
lokacija      2   55642   27821    3.14 0.0462 *
Residuals   147 1302325    8859                 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Rezultate dobijamo u vidu ANOVA tabele. U ovom jednostavnom slučaju analize varijanse imamo jedan faktor i jednu zavisnu varijablu. Za složenije modele sa više faktora, tabela će sadržati dodatne redove.

Prvi red prikazuje mere faktorskog varijabiliteta, dok drugi red sadrži mere rezidualnog varijabiliteta. F-statistika iznosi 3.14, uz odgovarajuću p-vrednost od 0.0462.

Nakon ANOVA analize, sprovodimo Tjukijev post-hoc test jednom linijom koda.

Prikaži kod 
tukey_test <- TukeyHSD(anova_model)

tukey_test
1
Funkcijom TukeyHSD sprovodimo Tjukijev post-hoc test nad prethodno definisanim modelom
2
Ispisujemo rezultate testa 
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = cena ~ lokacija, data = podaci)

$lokacija
                          diff         lwr      upr     p adj
Širi centar-Nova naselja 36.74  -7.8314172 81.31142 0.1280701
Uži centar-Nova naselja  44.00  -0.5714172 88.57142 0.0538469
Uži centar-Širi centar    7.26 -37.3114172 51.83142 0.9213366

Rezultati nam otkrivaju zanimljivu sliku. U ispisu vidimo tri reda koji prikazuju poređenja između grupa. Svaki red sadrži četiri ključne informacije:

  • diff: razlika između aritmetičkih sredina grupa
  • lwr: donja granica intervala poverenja od 95% za razliku
  • upr: gornja granica intervala poverenja od 95% za razliku
  • p adj: prilagođena p-vrednost za razliku dve aritmetičke sredine

Analiza pokazuje da je jedina razlika koja se približava statističkoj značajnosti ona između prosečne cene kafe u lokalima u užem centru grada i lokalima u novim naseljima. P-vrednost za ovu razliku iznosi NA, što je malo iznad 0.5, te možemo zaključiti da je razlika značajna samo na nivou \(p<0.1\). Na nivou uzorka, ta razlika iznosi 44 dinara u prosečnoj ceni kafe.

Faktorski varijabilitet koji smo otkrili ANOVA analizom proizlazi upravo iz ove razlike između lokala u užem centru i novih naselja. Za sva ostala poređenja nemamo dovoljno dokaza da bismo tvrdili da postoje značajne razlike u cenama kafe - drugim rečima, te razlike nisu dovoljno izražene u odnosu na varijabilnost cena unutar svake grupe.

Vraćajući se na početnu raspravu između dva studenta, možemo reći da su obojica delimično bili u pravu. Prvi student je ispravno primetio postojanje razlike u cenama između određenih delova grada, ali drugi student je takođe bio u pravu kada je ukazao na značajan varijabilitet cena unutar svake lokacije. ANOVA i post-hoc testovi nam omogućavaju da precizno kvantifikujemo ove odnose i bolje razumemo prirodu uticaja lokacije na cenu kafe.

10.7.1 Veličina efekta

U prethodnom delu videli smo da postoje relativno male razlike u prosečnoj ceni kafe između lokacija. Možemo li preciznije izmeriti ove razlike? Kao i kod t-testa, rešenje leži u konceptu veličine efekta.

Za kvantifikovanje veličine efekta u ANOVA analizi koristimo meru koja se naziva eta kvadrat (\(\eta^2\)). Eta kvadrat izračunavamo kao količnik faktorskog i ukupnog varijabiliteta. Vrednosti blizu 0 ukazuju na zanemarljiv uticaj faktora na zavisnu varijablu, dok vrednosti koje se približavaju 1 otkrivaju snažan uticaj faktora.

\[ \eta^2 = \frac{SS_{faktor}}{SS_{faktor} + SS_{rezidual}} \]

U našem slučaju, eta kvadrat iznosi:

Prikaži kod 
eta2 <- SSF / (SSF + SSR)

cat("Eta kvadrat: ", round(eta2, 2), "\n")
1
Izračunavamo eta kvadrat kao količnik faktorskog i ukupnog varijabiliteta 
Eta kvadrat:  0.04

Slično tumačenju korelacije i koeficijenta determinacije, postoje opšteprihvaćene granične vrednosti za interpretaciju eta kvadrata:

  • $0.01 ^2 $: mali efekat
  • \(0.06 < \eta^2 < 0.14\): srednji efekat
  • \(\eta^2 \geq 0.14\): veliki efekat

U našem primeru dobili smo mali efekat, što znači da faktor lokacije ima ograničen uticaj na cenu kafe u Novom Sadu. Ovaj rezultat je u skladu sa post-hoc analizom, koja je otkrila da je jedina značajna razlika u cenama između lokala u užem centru grada i novih naselja. Eta kvadrat nam precizno pokazuje da lokacija objašnjava samo 4% ukupne varijabilnosti u cenama kafe.

10.8 ANOVA i regresija

Analiza varijanse je fundamentalni alat za razumevanje statističkih modela. Ona nam omogućava da razdvojimo varijabilitet koji pripisujemo nezavisnoj varijabli od varijabiliteta koji potiče iz drugih izvora: slučajnosti i dejstva neidentifikovanih ili nekontrolisanih faktora.

Ako pažljivo razmislimo, ovaj cilj je gotovo identičan ciljevima metoda koje smo ranije obradili u ovom udžbeniku. F-test smo već susreli u poglavlju o regresiji (odeljak Odeljak 8.8). Vreme je da otkrijemo njegovu pravu prirodu.

Hajde da ponovo konstruišemo regresioni model iz tog poglavlja.

Prikaži kod 
podaci_reg <- read.csv("https://gist.githubusercontent.com/atomashevic/1ea72e8ea912083492b60af7ecd07fbf/raw/7d658eb07d321126989acf774a8428dc712bfc9d/zdravstvo.csv")

model_reg <- lm(kvalitet ~ budzet, data = podaci_reg)

summary(model_reg)

Call:
lm(formula = kvalitet ~ budzet, data = podaci_reg)

Residuals:
    Min      1Q  Median      3Q     Max 
-29.523 -11.245  -0.986   9.639  36.324 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 4.907e+01  4.073e+00   12.05  < 2e-16 ***
budzet      3.170e-03  7.354e-04    4.31  6.4e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 14.77 on 58 degrees of freedom
Multiple R-squared:  0.2426,    Adjusted R-squared:  0.2295 
F-statistic: 18.58 on 1 and 58 DF,  p-value: 6.404e-05

Vidimo da F-statistika iznosi 18.58, uz stepene slobode 1 i 58. P-vrednost ovog testa je veoma blizu nule (6.404e-05, što je zapravo 0.00006404). Ovo nas direktno vraća na ANOVA analizu. Tačnije, regresija je specifičan slučaj ANOVA analize gde faktor predstavlja kontinuiranu kvantitativnu varijablu.

ANOVA nalazi svoju primenu i pri analizi regresionog modela. Kada konstruišemo regresioni model, varijabilitet zavisne varijable možemo razdvojiti na deo koji je objašnjen regresionim modelom i deo koji nije. ANOVA analiza nam omogućava da precizno procenimo koliko faktor (nezavisna varijabla) doprinosi objašnjenju varijabiliteta zavisne varijable. Sam postupak razlaganja varijabiliteta je identičan kao u primeru koji smo demonstrirali u ovom poglavlju, što znači da je i primena u R-u gotovo ista.

Koristićemo ponovo funkciju anova(), pri čemu je jedini ulazni parametar regresioni model.

Prikaži kod 
anova_reg <- anova(model_reg)

anova_reg
Analysis of Variance Table

Response: kvalitet
          Df  Sum Sq Mean Sq F value    Pr(>F)    
budzet     1  4052.2  4052.2  18.576 6.404e-05 ***
Residuals 58 12652.4   218.1                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Vidimo da je regresiona ili faktorska varijansa 18 puta veća od rezidualne, što ukazuje na to da je ovaj regresioni model uspešno objasnio varijabilitet zavisne varijable. Ovo predstavlja dodatni korak u dijagnostici regresionog modela.

U poređenju sa klasičnom analizom varijanse, u ovom specifičnom regresionom slučaju stepeni slobode odgovaraju broju nezavisnih varijabli u modelu. Pošto imamo jednu nezavisnu varijablu, faktorski stepen slobode je 1, a rezidualni stepen slobode je 58. Drugim rečima, umesto broja grupa, \(k\) označava broj nezavisnih varijabli u modelu. Takođe, primena post-hoc analize nema smisla u ovom slučaju jer nemamo diskretno definisane grupe koje bismo mogli analizirati.

Ipak, činjenica da se regresija može posmatrati kao poseban slučaj analize varijanse otkriva nam dublju povezanost ovih metoda. Tu vezu ćemo detaljnije istražiti u završnom poglavlju ovog udžbenika, gde ćemo otkriti jednu neočekivanu istinu skrivenu u samom nazivu udžbenika.

10.8.1 Lična karta metoda: ANOVA

Šta radi? Testira postojanje uticaja faktora na zavisnu varijablu, tj. provera da li postoje statistički značajne razlike između aritmetičkih sredina grupa.

Kada koristiti? Kada imamo više od dve grupe i želimo da proverimo da li postoji statistički značajan uticaj faktora na zavisnu varijablu.

Koliko varijabli imammo? Jedna kategorijalna varijabla (faktor) i jedna kvantitativna varijabla (zavisna).

Kako glase hipoteze? Nulta hipoteza tvrdi da ne postoji razlika između aritmetičkih sredina grupa, dok alternativna hipoteza tvrdi da postoji bar jedna grupa koja se razlikuje od ostalih.

Kako izgleda statistika testa? Koristimo F-test da testiramo odnos između faktorske i rezidualne varijanse.

\[ F = \frac{SS_{faktor} / df_{faktor}}{SS_{rezidual} / df_{rezidual}} \]

Kako računamo p-vrednost? P-vrednost se računa kao površina ispod krive F-distribucije koja se nalazi desno od naše F-statistike.

10.9 Zadaci

U ovom zadatku koristimo podatke iz komparativnog istraživanja sa prostora bivše Jugoslavije. Istraživači su merili stepen jugonostalgije kod ispitanika na skali od 0 („Ne osećam nostalgiju prema vremenu nekadašnje Jugoslavije“) do 10 („Osećam veliku nostalgiju prema vremenu nekadašnje Jugoslavije“). Ispitanici su podeljeni u 4 grupe prema državi iz koje dolaze: Srbija, Hrvatska, Crna Gora i Slovenija.

Koristeći varijable drzava i jugonostalgija, sprovedite analizu varijanse i post-hoc testove kako biste utvrdili postoje li statistički značajne razlike u stepenu jugonostalgije između građana različitih država.

Razmislite: Kako u ovom slučaju interpretiramo dejstvo faktora i po čemu se ono razlikuje od primera sa cenama kafe koji smo obradili ranije?

Podatke možete učitati na sledeći način:

Prikaži kod 
podaci <- read.csv("https://gist.githubusercontent.com/atomashevic/51ec08bc58476230f59f51ef7435efaa/raw/27e3ee1ad8f783ec6b040874b000784d2fe96c40/jugonostalgija.csv")

U ovom zadatku analiziramo podatke o subjektivnom zadovoljstvu životom (subjektivnom blagostanju) građana sa različitim stepenima obrazovanja. U istraživanju su definisane četiri grupe ispitanika prema stepenu obrazovanja:

  1. bez završene osnovne škole
  2. završena osnovna škola
  3. završena srednja škola
  4. završen fakultet ili visoka škola

Koristeći varijable obrazovanje i zadovoljstvo, potrebno je sprovesti analizu varijanse i post-hoc testove kako bi se utvrdilo postojanje statistički značajnih razlika u subjektivnom blagostanju između grupa ispitanika sa različitim nivoima obrazovanja.

Podatke možete učitati na sledeći način:

Prikaži kod 
podaci <- read.csv("https://gist.githubusercontent.com/atomashevic/c3189aa3191a7c7c2306bb726f1cb80d/raw/d7472ad5736d165a3084a4f3c5b028818c111447/obrazovnje-zivot.csv")

U podacima iz prethodnog zadatka uočavamo problem - nije ispunjena pretpostavka o homogenosti varijanse između grupa. Variance zadovoljstva životom značajno se razlikuju među grupama. Ovo može biti posledica nekog nekontrolisanog faktora koji nismo uzeli u obzir ili jednostavno priroda uticaja obrazovanja na zadovoljstvo životom.

Za prevazilaženje ovog problema, potrebno je ponoviti analizu koristeći Velčov ANOVA metod (eng. Welch’s ANOVA). Ovaj metod je elegantan jer ne zahteva pretpostavku o homogenosti varijanse između grupa.

Velčova ANOVA je modifikacija standardne ANOVA analize koja koristi korekciju za različite varijanse grupa. U R-u je implementirana kroz funkciju oneway.test() sa parametrom var.equal = FALSE.

Sprovedite analizu koristeći Velčov metod i nakon toga uradite post-hoc testove. Obratite posebnu pažnju na sledeća pitanja: - Kakve razlike između grupa otkriva ova analiza? - Da li možemo govoriti o linearnom uticaju obrazovanja na zadovoljstvo životom?

Konzola za rešavanje zadataka